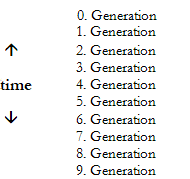
Grundlagen: "totalistische" zelluläre Automaten

Ein zellulärer Automat besteht aus einer Menge von Zellen die jede einen definierten, meistens diskreten Zustand hat (Anfangszustand). Eine Regel, die den Zustand der Zelle und endlich vieler Nachbarzellen berücksichtigt, bestimmt den Zustand der Zelle in der nächsten Generation. Die Zellen können auf einer Linie (1-dimentional) auf einer Fläche (2-dimensional) oder auch in höheren Dimensionen angeordnet sein.

Einer der bekanntesten zellulären Automaten ist das Game of Life von John Conway aus den 1970er Jahren. Hier sind die Zellen auf einer Fläche, also 2-dimensional, angeordnet.

GeZa dagegen behandelt ausschließlich 1-dimensionale Zellularautomaten, d.h. die Zellen sind entlang einer Linie aufgereiht. Die einzelnen Generationen werden als einzelne Zeilen  untereinander dargestellt. Man kann also auf der Fläche des Bildschirms gleichzeitig die räumliche und zeitliche Entwicklung darstellen. Hier am Beispiel der Regel 0100, bzw. 01 (nicht aufgeführte Stellen werden automatisch mit Nullen aufgefüllt:


 

Eine Zelle kann nur den Zustand 0 (=weiß) oder 1 (=grün) besitzen.
Als Anfangszustand (=0. Generation) wurde eine Zelle auf 1 (grün), alle andern auf 0 (weiß) gesetzt.
Die Regel 01 (3 Zellen-Modus) bedeutet dabei folgende Berechnungsvorschrift für die Bildung der nächsten Generation:

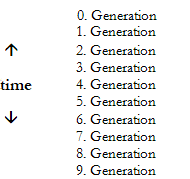
Summe von 3 benachbarten Zellen (links,Mitte,rechts)

0

1

2

3

Zustand der mittleren Zelle in der nächsten Generation

0

1

0

0

Dies ist eine links/rechts-symmetrische Regel. Zellularautomaten deren Regel  nur von der Summe der Nachbarzellen abhängen werden "totalistisch" genannt.
Die Ziffer an der n-ten Position der Regel gibt den Zustand der neuen Zelle an, wenn die Summe der 3 Nachbarzellen n-1 ist. Ist die Summe beispielsweise 3, so erhält die Zelle in der nächsten Generation den Wert der 4. Stelle in der Regel. Ist die Stelle nicht vorhanden wird Null gesetzt. Diese Schreibweise weicht von der von Stephen Wolfram verwendeten ab.
Sieben zusätzliche Zeichen haben die folgende spezielle Bedeutung:

Zeichen
 Bedeutung
=
 Die Zelle behält ihren Wert.
+
 Der Wert der Zelle wird um 1 erhöht, aus 9 wird Null.
-
 Der Wert der Zelle wird um 1 erniedrigt, Null bleibt Null.
!
 Aus Null wird 1, ansonsten erhält die Zelle den Wert Null.
?
 Die Zelle erhält einen zufälligen Wert.
>
 Die Zelle erhält den größten Nachbarzellenwert.
<
 Die Zelle erhält den kleinsten Nachbarzellenwert.


Inhaltsverzeichnis          Wolfram        NaSch-Modell