fundamentals Zhabotinsky
The name of this CA is based on the Belousov-Zhabotinsky-reaction, a well known chemical oszillator.
To simulate this chemical reaction i used the "Misch-Masch-Maschine" by Martin Gerhardt and Heike Schuster:
cells may have states of 0 (healthy), 1 to 255 (infected) and 256 (ill).
A cell of state 0 (healthy) will get the state [K/k1] + [I/k2] in the next generation.
K=sum of ill neighbors, I=sum of infected neighbors,
k1 = illness threshold (1-5), k2 = infect threshold,
the square brackets rounding off to integer.
Infected cells (state 1-255) go to [S/A] + g, but max 256 in the next generation.
S = sum of the values from all neighbors and the cell itself. A is the number of these cells. [S/A] is just the mean value.
g = constant (1-120) allways added, it is a kind of stimulation.
An ill cell (state 256) will be healthy (state 0) in the new generation.
This automaton is neighborhood with r=4. 
This process may be described in this words:
- healthy cells will be infected by infected and ill neighbors.
- infected cells are powered by a mechanism of stimulation and diffusion until the cell is ill.
- "ill" cells will be healthy immediately and the process starts again.
There are generated a lot of pattern, depending of the parameter k1, k2, and g, but of the starting states also.
Below you see 2 typical examples:
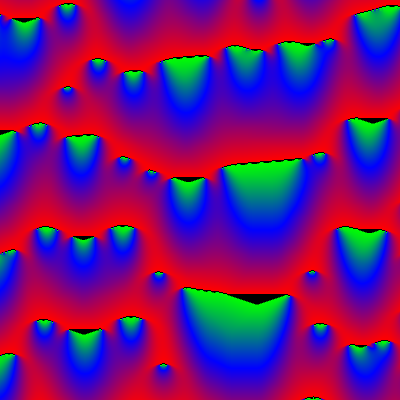
k1=1, k2=2, g=2

k1=1, k2=2, g=30


