Grundlagen Zhabotinsky
Der Name dieses Zellularautomaten geht zurück auf einen chemischen Oszillator der Belousov-Zhabotinsky-Reaktion,
Zur Simulation dieser chemischen Reaktion habe ich die "Misch-Masch-Maschine" von Martin Gerhardt und Heike Schuster verwendet.
In GeZA ist der Algorithmus auf 1-dimensionale Verhältnisse angepasst.
Die originale 2-dim-Version finden Sie in der App GeZA-2D!
Zellen können Werte zwischen 0 (gesund), 1 bis 255 (infiziert) und 256 (krank) annehmen.
Wenn eine Zelle den Wert 0 hat (gesund) wird ihr für die neuen Generation der Wert [K/k1] + [I/k2] zugewiesen.
wobei K die Anzahl der kranken Nachbarn und I die Anzahl der infizierten Nachbarn ist.
k1 ist die Krank-Schwelle (1-5), k2 ist die Infekt-Schwelle (1-5).
Die eckigen Klammern [] sagen, dass der Wert abgerundet wird.
Infizierte Zellen (Wert 1-255) wird für die neue Generation [S/A] + g, maximal 256, zugewiesen.
S ist die Summe der Werte aller Nachbarzellen und der Zelle selbst. A
ist die Anzahl der Zellen. [S/A] ist praktisch der Mittelwert.
g ist ein konstanter Faktor (1-120) der immer hinzu addiert wird, so etwas wie eine Anregung.
Eine kranke Zelle (Wert = 256) ist in der neuen Generation gesund (Wert = 0).
Bei diesem Automaten wird die Nachbarschaft mit r=4  verwendet.
verwendet.
Mit anderen Worten kann man den Ablauf so beschreiben:
- Gesunde Zellen werden durch infizierte und kranke Nachbarzellen infiziert.
- auf infizierte Zellen wirkt ein Mechanismus aus Anregung und Diffusion bis diese "krank" wird.
- "kranke" Zellen werden sofort wieder gesund und es geht von vorne los.
Es können eine Vielzahl von Mustern, abhängig von Parametern k1, k2, und g, sowie den Anfangsbedingungen, entstehen.
Unten sind 2 typische Beispiele:
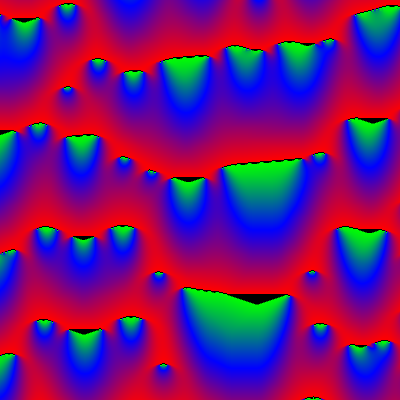
k1=1, k2=2, g=2

k1=1, k2=2, g=30
 verwendet.
verwendet.
